
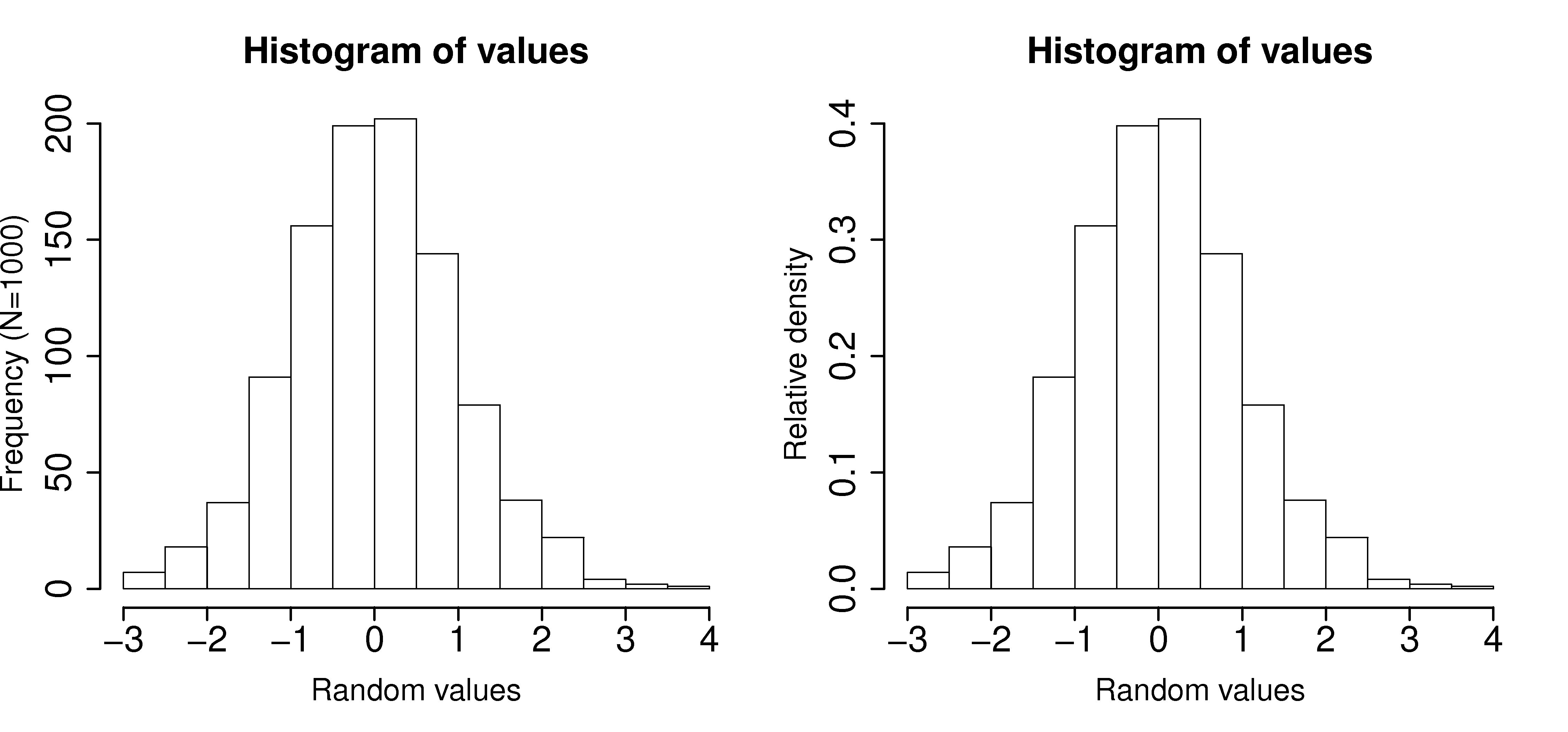
The long-term sex ratio at birth 1.06:1 (boy:girl) is expected in Canada but a newly pregnant mother would not know the sex. Let us contrast some long-term and short-term expectations next: Probabilities can be used to describe our long-term expectations. This is why concepts of chance and random phenomena can be use to described systems and processes. In preparing the above histograms, what have you implicitly inferred about time-scales? These histograms show the long-term distribution (probabilities) of the system being considered. The annual income for people in your country.Īnalytical measurements taken in a laboratory, by the same person or computerized process. The grades for a class for a really easy test. Try creating a fictitious histogram for each of the following situations: Plt.ylabel("Number of packages (N=)".format(N)) # with a mean of 1100 and standard deviation If the variability in the packaging system could be reduced - the spread of the data made narrower - then the histogram can be shifted to the left, thereby reducing overfill. Notice how the packaging system has to overfill each carton so that the vast majority of packages weigh over 1 kg (what is the average package mass?). The continuous variable, mass, is divided into equal-size bins that cover the range of the available data. Here is an example showing the mass of cartons of 1 kg of flour. Histograms make sense for categorical variables, but a histogram can also be derived from a continuous variable. In this case Female and Male represent the two categories. The raw data in the above example was a vector that consisted of 2739 text entries, with 1420 of them as Male and 1319 of them as Female. For example: number of children born, categorized against their birth gender: male or female. It shows the number of samples that occur in a category: this is called a frequency distribution. This section aims to show how we can visualize and quantify any variability in a recorded vector of data.Ī histogram is a summary of the variation in a measured variable. The previous section has hopefully convinced you that variation in a process is inevitable. Histograms and probability distributions ¶ Product development and product improvementĢ.4. Applications of Process Improvement using Data Analysis of designed experiments using PLS models Variability explained with each component

A mathematical/statistical interpretation of PLS Advantages of the projection to latent structures (PLS) method Introduction to Projection to Latent Structures (PLS) Visualization latent variable models with linking and brushing Using indicator variables in a latent variable model Determining the number of components to use in the model with cross-validation Algorithms to calculate (build) PCA models Preprocessing the data before building a model Interpreting loadings and scores together More about the direction vectors (loadings) Extended topics related to designed experiments Blocking and confounding for disturbances Highly fractionated designs: beyond half-fractions Generators: to determine confounding due to blocking Generating the complementary half-fraction Example: analysis of systems with 4 factors Assessing significance of main effects and interactions Example: design and analysis of a three-factor experiment Analysis of a factorial design: interaction effects Analysis of a factorial design: main effects Changing one single variable at a time (COST) Experiments with a single variable at two levels Design and analysis of experiments in context Outliers: discrepancy, leverage, and influence of the observations More than one variable: multiple linear regression (MLR) Summary of steps to build and investigate a linear model Least squares models with a single x-variable The industrial practice of process monitoring Statistical tables for the normal- and t-distribution
The normal distribution and checking for normality General summary: revealing complex data graphically


 0 kommentar(er)
0 kommentar(er)
